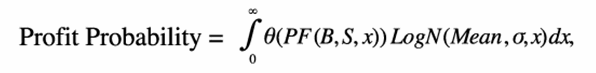Когда волатильность опционов искажает вероятность

Сергей Израилевич и Вадим Цудикман
Современные теории опционного ценообразования - от моделей Блэка-Шоулза до продвинутых математических алгоритмов – основаны на концепции вероятностей.
Одним из самых популярных индикаторов, используемых для оценки инвестиционной привлекательности как отдельный опционов, так и их сочетаний, является индикатор вероятности получения прибыли (ВПП). Он выражает вероятность того, что во время истечения опциона (или в любой другой момент до его истечения) данный опцион принесет прибыль. Является ли функция прибыльности (математическое ожидание выигрыша) положительной или отрицательной, определяется будущей ценой базового актива.
Применяя классическую теорию вероятности, ВПП опциона можно рассчитать путем совмещения результата комбинации функции прибыльности и плотности распределения вероятностей для ценовых диапазонов, для которых функция прибыльности является положительной:

　
Где x - цена базового актива; PF(B,S,x) - функция прибыльности комбинации S с базовым активом B; LogN(Mean,σ,x) - плотность распределения вероятностей (или функция плотности вероятности) логарифмически нормального распределения с параметрами Mean (математическое ожидание цены); и изменение σ; θ(y) - тета-функция с аргументом y = PF(B,S,x), который имеет следующие значения: θ(y) = 1, если y > 0, и θ(y) = 0 в других случаях.
Эта формула применима в тех случаях, когда цена воспринимается как непрерывная переменная.

В дискретном случае, конечное ценовое множество{xt,t = t1, t2, …, tn} заменяет непрерывную переменную. Эта совокупность цен включает все возможные будущие значения цены.
Множество вероятностей {p(xti,t),i = 1, 2, …, n}, заданных соответствующим ценовым значениям, заменяет функцию плотности вероятности.
Ценовой индекс i формирует два подмножества:
I+ = {i : PF(B, S, Xt1) > 0}, где функция прибыльности положительна, и I- = {i : PF(B, S, Xt1) ≤ 0}, где функция прибыльности отрицательна или равна нулю. Вероятность получения прибыли можно рассчитать как сумму вероятностей всех элементов первого подмножества:
 

Оценка прибыльности
Вероятность получения прибыли (ВПП) широко используется трейдерами и включена практически в любое ПО, разработанное для анализа опционов. Данный индикатор является одним из главных критериев, заложенных в основу различных программ, разработанных для расчета потенциальных торговых возможностей появляющихся на опционных рынках. Этот индикатор популярен в силу простоты его расчета и высокой эффективности на практике. В сочетании с другим важным индикатором, ожидаемой прибылью, ВПП дает возможность точно рассчитать вероятность.
В то же время, на основании долгих наблюдений, ВПП при использовании для short-опционов может быть сильно переоценена в периоды высокой волатильности.
Ни для кого не секрет, что открытие коротких позиций по опционам является одной из самых рисковых опционных стратегий. В периоды высокой волатильности, и особенно во время финансовых кризисов, риск, заложенный в этой стратегии, возрастает во много раз.
По той причине, что переоцененная ВПП неизбежно ведет к недооценке рисков, очень важно определить степень влияния волатильности базового актива на значения вероятности.
Чтобы выполнить эту задачу, проводились статистические исследования на основе базы данных цен опционов и их базовых активов за пятилетний период (2005-2010). На данном историческом участке встречались как спокойные, так и экстремальные рыночные движения (достаточно вспомнить последний финансовый кризис). На основании этих данных был выполнен горизонтальный и вертикальный анализ, включая соотношение между ВПП и волатильностью базового актива.
В вертикальном анализе 1000 самых ликвидных рынков акций США были использованы в качестве базовых активов. Для каждого из них мы открыли 3 коротких стрэддла (используя страйк-цены, которые были самыми близкими к текущей цене базового актива*) для 1-й, 2-й и 3-й недели до истечения опционов. Все комбинации опционов (стрэддлы) должны были истечь в сентябре 2010. Всего мы оценили 3000 коротких стрэддлов.
Для горизонтального анализа были выбраны акций пяти компаний, опционы на которые пользовались большой популярностью у трейдеров: Apple, Boeing, Ford Motor, General Electric и IBM. Для каждого из пяти рынков каждый день в течение пяти лет открывался один короткий стрэддл. По аналогии с вертикальным анализом, стрэддлы открывались по самым ликвидным опционным контрактам (с ближайшей датой истечения и ближайшей страйк-ценой к текущей цене базового актива). Для каждой комбинации была рассчитана ВПП для значений исторической и подразумеваемой волатильности. То есть всего было оценено 6000 комбинаций.
“Profit probability vs volatility” (рис. ниже – ВПП и волатильность) иллюстрирует отношение между ВПП и подразумеваемой волатильностью. И горизонтальный и вертикальный анализ показал, что ВПП возрастает при увеличении волатильности. Хотя эта соотношение и не такое уж сильное (коэффициент корреляции варьируется от 0.36 до 0.66), во всех случаях оно статистически важно. В периоды экстремальной волатильности (кризисы) ВПП возрастает на 80-90%, а в некоторых случаях даже на 100%. Очевидно, что такие расчеты не являются полностью объективными. Интуиция и опыт последних финансовых кризисов подсказывают, что в периоды слишком сильной рыночной волатильности вероятность получить прибыль от коротких опционов скорее снижается, чем повышается.
Если дело обстоит именно так, то как же тогда объяснить существование прямой зависимости между прибыльностью и волатильностью?

Решение загадки
Чтобы найти решение, мы сопоставили временную динамику подразумеваемой и исторической волатильности. Обычно считают, что во времена кризисов опционные премии (и следовательно, подразумеваемая волатильность) резко возрастают, потому как неопределенность и беспокойство участников рынка растет тоже. Хотя историческая волатильность также растет, это происходит медленнее и с очевидным запаздыванием.
“Trends in volatilities” (рис. ниже) изображает это явление на примере графика акций компании Боинг:

Дивергенция циклов двух типов волатильности наблюдается, потому что во время кризиса сильно возрастают опционные премии, в то время как историческая волатильность растет медленнее. Это происходит потому, что она рассчитывается на основании исторических данных, которые включают ценовые значения из предыдущих, менее волатильных периодов. Более высокие премии подразумевают более высокие значения функции прибыльности; относительно низкая историческая волатильность подразумевает более низкое изменение, используемое в логарифмически нормальной функции плотности вероятности. Как видно из вышеупомянутых формул, оба фактора вызывают рост ВПП на более высоких уровнях подразумеваемой волатильности.
Неоправданно завышенные значения ВПП, полученные в периоды высокой волатильности, не подходят для оценки прибыльности опционных портфелей, содержащих короткие опционы. Необходимо разработать методы, позволяющие подгонять ВПП под текущий уровень волатильности.
Существует несколько подходов к решению данной проблемы:
•Расчет исторической волатильности, используемой как переменная для построения функции плотности вероятности, основан на последовательности исторических ценовых значений определенной длительности. Чем более длительна эта последовательность, тем сильнее влияние предыдущих данных (тех, которые относятся к более спокойным периодам рыночной активности) и тем больше различие в циклах исторической и подразумеваемой волатильности. Это приводит к завышенной оценке ВПП. Степень искажения в оценке вероятности может быть существенно снижена путем регулирования параметра “длительность ценовой последовательности” в соответствии текущим уровнем подразумеваемой волатильности. Этот параметр следует изменять обратно пропорционально по отношению к волатильности.
•Стандартный метод, используемый для расчета исторической волатильности, основан на исторических ценовых значениях, каждое из которых имеет свой вес (значимость) по отношению к остальным. В качестве альтернативы можно рассмотреть дифференциальное применение коэффициентов значимости (веса) по аналогии с тем, чтобы мы делали при расчетах экспоненциального скользящего среднего (EMA) в отличие от простого скользящего среднего (SMA). Более поздние цены обладали бы большим удельным весом (значимостью) по отношению к более ранним. В результате недавние ценовые колебания имели бы большее влияние на изменение (изменчивость) по сравнению с более ранними ценовыми колебаниями. Функция, задающая вес (значимость) может быть любой формы: линейная, экспоненциальная и т.п.
•Одним из основных факторов, определяющих функцию прибыльности определенной комбинации опционов, является премия, заработанная трейдером в качестве дохода от открытия короткой позиции. Во время кризисов премии растут быстрее, чем историческая волатильность, что приводит к дивергенции двух типов волатильности и искажению вероятности. Поэтому, чтобы получить объективную ВПП, нужно сократить дивергенцию между этими двумя типами волатильности путем искусственного уменьшения параметров функции прибыльности. Это можно сделать путем введения специального коэффициента настройки, который бы занижал значения премии на какую-то фиксированную величину или на определенное значение коэффициента.
Высокая волатильность - это уже данность на современных рынках. Более того, она зачастую проявляется без предупреждения, внезапно. Для трейдера очень важно вовремя заметить это и адаптировать свою технику анализа в соответствии с текущими изменениями.
Методы, которые мы обсудили, являются достаточно эффективными в плане решения проблемы искажения ожидаемой прибыльности по открытым опционным позициям.
Сергей Израилевич и Вадим Цудикман являются авторами работы под названием “ Систематическая торговля опционами” (“Systematic Options Trading” - Financial Times Press, 2010), где можно найти более подробное описание того, как применять индикатор расчета вероятности получения прибыли в опционной торговле, а так же методы определения оптимальных параметров данного индикатора.

*) Cтрайк-цены, самые близкие к текущей цене базового актива – имеются в виду так называемые стрэддлы ATM. Понятие «стрэнглы/стрэддлы ATM» было ввёдено на тренингах «Опционы с нуля» (торговля волатильностью) и активно используется в торговле.

Комментарий руководителя факультета опционов Александра Комарских:
Авторы статьи обсуждают применение в опционной торговле так называемых «механистических подходов». В опционной торговле мы наблюдаем, как достаточно сложная научная математическая дисциплина «приходит на помощь» рядовому трейдеру. Математические модели опционов прочно вошли в повседневность и предоставляют много очень полезной и важной информации. К сожалению, последний экономический кризис наглядно показал, к чему может привести слепое следование «машинным» расчётам. Одной из основных причин кризиса называется как раз неверный расчёт риска инвестиционных финансовых инструментов. Опционы, конечно, являются как раз таковыми.
Опционные продажи всегда являлись наиболее привлекательными и наиболее рискованными для начинающих трейдеров. Тактика «продай и получи лёгкие деньги» явилась одним из катализаторов развития последнего кризиса. Именно поэтому затронутая тема очень актуальна. Авторы, проведя крупное исследование, показывают, что в любой «механистической» торговле важно использовать более глубокий анализ исторических данных с корректировкой расчётных величин, причём, зачастую требуется вмешательство, основанное на опыте трейдера. Более того, фактически доказано, что продавать неожиданно высокую волатильность может оказаться даже значительно более рискованно, чем торговать в средних диапазонах. На мой взгляд, это один из наиболее значимых моментов данной статьи.
Авторы не первый раз обращаются к теме опционов (в том числе в сфере инвестиций) и делают это очень профессионально, что делает их мнение значимым и полезным для всех опционных трейдеров.