Математическое моделирование финансовых систем открытых рынков состоит из комплексного системного анализа, включающего как сбор информации о системе и анализ ее причинно-следственных связей, так набор аналитических методов системного анализа и оценки соответствия имитационных моделей реальным процессам.
Основой методов системного анализа процесса формирования валютного курса является составление математической модели, для чего применяются методы теории систем и принятия решений, теории оптимального управления, функционального анализа и дифференциальных уравнений. Кроме того, особый интерес представляет исследование изменения свойств систем открытых рынков в зависимости от динамики параметров, входящих в эту систему. На эффективность этих методов существенно влияет выбор подходящей замены входящих в систему переменных.
Статистические методы оценки используются в тех случаях, когда доступна база статистических данных анализируемых рисковых событий или изменений факторов риска для валютного курса. На основе статистических данных рассчитывается частота возникновения потерь определенного уровня. Частота возникновения определенного уровня потерь рассчитывается путем деления числа соответствующих случаев на их общее число (включая положительные исходы). В случае большого количества данных частоту можно приравнять к вероятности возникновения потерь и по этим данным построить кривую риска, которая дает наиболее полное представление о риске. Для каждой дискретной зависимости "вероятности-потери", полученной таким образом, в целях ее аппроксимации может быть подобрана непрерывная функция соответствующего вида. Для рядов данных по различным видам ущерба чаще всего используются три вида функций: нормальная (или гауссовская), экспоненциальная (больцмановская) и самоподобная (функция Парето).
Большинство рисков возникает как результат действия большого числа независимых случайных факторов и поэтому могут быть описаны нормальным распределением. Данному условию, как правило, удовлетворяют: потери от операций на финансовом рынке, отказы и аварии технических систем. Самоподобное распределение характерно для большинства природных катастроф, таких, как землетрясения и наводнения. Больцмановское распределение является промежуточным типом между двумя предыдущими.
Для получения интервальной оценки финансовых рисков (рыночного, кредитного, риска ликвидности) широко используется методика под названием стоимость под риском (Value-at-Risk, VaR), основанная на распределении вероятностей. За последнее десятилетие методика VaR стала одним из самых популярных методов оценки риска, чему послужило несколько причин. Первой причиной стало раскрытие в свободное пользование методики оценки риска. Вторая причина связана в инвестиционными потерями в конце 1990-х гг., от операций с производными финансовыми инструментами. Третья причина – это использование величины VaR для определения резервного капитала. В рамках методики VaR для построения распределения вероятностей случайной величины используется три метода: аналитический, исторического моделирования и статистических испытаний Монте-Карло.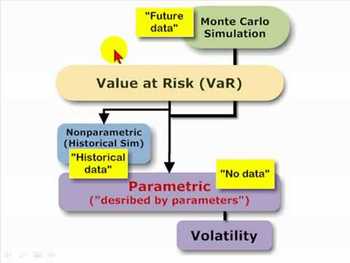
Под термином VaR понимают как методику (совокупность отдельных методов) оценки рисков, так и количественную оценку риска в виде единственного параметра–VaR. Параметр VaR это максимально возможная величина потерь открытой позиции, но которая однако не будет превышена в течение заданного времени с указанной вероятностью. При расчете VaR задаются параметры: период времени, на который рассчитывается риск, и доверительная вероятность (как правило, 95–99%) затем, используя распределение вероятностей, определяется параметр VaR, т.е. числовое значение потерь, которое соответствует этой вероятности.
Например, инвестор имеет открытую валютную позицию в размере 10 млн долл. Как определить валютный риск позиции? В соответствии с принятым определением риска в первую очередь необходимо сформулировать, что является неблагоприятным событием, вероятность наступления которого (риск) мы оцениваем. Допустим, мы будем оценивать риск снижения стоимости позиции под влиянием изменения валютного курса на 5% и более, т.е. на 0,5 млн долл. и более. Определив вероятность снижения стоимости валютной позиции на сумму ≥ 0,5 млн долл., мы оценим валютный риск. Допустим, эта вероятность составляет 2%. Тогда можно сказать, что риск снижения стоимости открытой валютной позиции на 0,5 млн долл. и более равен 2%, или, другими словами: с доверительной вероятностью 98% снижение стоимости не превышает 0,5 млн долл.
Методика VaR за исходный параметр берет доверительную вероятность (как правило, 95–99%) и затем определяет параметр VaR, то есть числовое значение потерь (или другой рассматриваемой случайной величины), соответствующее этой вероятности. Возвращаясь к примеру с валютной позицией, используя методику VaR, мы с доверительной вероятностью 98% оцениваем максимально возможное снижение стоимости и получаем то же число VaR = 0,5 млн долл.
Литература
[1]. Моисеев Н.Н. Математические задачи системного анализа. – М.: Наука, 1981, 487 с
2. Соболев В.В. Валютный дилинг на финансовых рынках/ Юж.-Рос. гос. техн. ун-т (НПИ). – Новочеркасск, 2009. – 442 с.
3.Струченкова Т.В. Валютные риски: Учебное пособие. М.: Финакадемия, 2009. 160 с. 4.Соболев В.В. Математическое моделирование вероятности достижения уровня в задаче экстраполяции // Fortrader.ru - 2011. - № 1 (67). - С. 76-79.
5. Якимкин В.Н. Новый подход к прогнозированию на рынке Forex. М.: SmartBook, 2008.
