 В.В.Соболев, к.т.н., Южно-Российский государственный технический университет
В.В.Соболев, к.т.н., Южно-Российский государственный технический университет
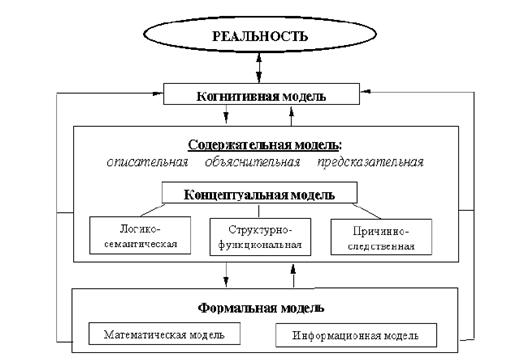
Существует множество специфических постановок задач моделирования валютного курса и путей их решения. Тем не менее, среди них можно выделить нечто общее, обязательное – этапы, в той или иной степени, реализуемые при построении большинства математических моделей. Этапы можно представить пятью блоками, границы которых ограничены тем более строгими линиями, чем сильнее эти этапы могут быть «алгоритмизированы».
Этапы моделирования
Сама процедура моделирования в общем случае представляет собой не прямую дорогу к цели, а неоднократный возврат на уже пройденные ступени, их повторение с подправленными данными – последовательное приближение к удовлетворительному варианту. В общем случае все начинается с оценки реальной ситуации с позиций имеющейся априорной модели и цели (1 этап), в результате формируется содержательная модель (2 этап), отражающая постановку задачи. Содержательная модель формируется на «родном» языке задачи: механики, физики, экономики, биологии, социологии и т.д. Затем выбирается структура модели – наиболее подходящий математический аппарат, вид и число уравнений, вид функций (3 этап). На следующем, 4-м этапе, если это требуется, конкретизируются детали модели (делаются необходимые аппроксимации, подгоняются коэффициенты уравнений) и, наконец, на 5-ом этапе с помощью критериев, выбор которых диктуется целью моделирования, проверяется качество получившейся конструкции. Если качество модели неудовлетворительно, процедура повторяется с начала или с промежуточного этапа, и делается следующее приближение.
Обман чувств и интуиция трейдера могут привести к ложным представлениям о рынке, хотя его интуиция стремится к тому, чтобы не только иметь правильные мысли, но и соответствующие впечатления. Именно ощущение действительности и правильные представления о ней поставляют информацию для интуиции. Интуиция предполагает наличие внимания и открытости. Чтобы быть способным на это, человек должен быть свободен и уверен в себе. Несмотря на любые задачи, которые необходимо выполнять, он остается таковым до тех пор, пока испытывает чувство внутренней свободы и удовлетворение.
Несмотря на всю неопределенность, царящую в торговом мире, инвестор будет чувствовать себя гармонично, если он сможет обрести уверенность в себе и самоуважение. Люди воспринимают не непосредственно наблюдаемый объект, а информацию о нем, которую дают органы чувств, т.е. получают не картину объективной реальности, а картину отношений между человеком и реальностью. На основе чувственного восприятия формируются образные модели. Образы могут формироваться в процессе обучения (в семье, школе, вузе, компании) или в процессе собственной практики (научной деятельности, участия в производстве). Соответствие образов реалиям приходится контролировать с учетом погрешностей чувственного восприятия, возможных заблуждений учителя, ошибочности сложившихся на данном этапе исторического развития научных представлений и т.п. Многие примеры демонстрируют ненадежность информации, получаемой через органы чувств и чувственной интуиции, той интуиции, которая формируется как результат взаимосвязи опыта, чувственных восприятий и грубых догадок.
Интуиция качественно меняется, если опирается на научное знание и, в первую очередь, на математику. Например, научный анализ движения на основе понятий динамики позволяет более правильно ответить на вопрос: как должно быть направлено ружье при стрельбе в мишень, которая начинает падать в момент выстрела; или куда упадут ключи, выпавшие на ходу у вас из руки. Чувственная интуиция подсказывает варианты наклонить ствол к земле, а ключи искать где-то сзади. Научный же анализ говорит о том, что ствол должен быть горизонтален, и направлен в начальную точку расположения мишени, а ключи упадут у ноги, как если бы вы стояли. С опытом научного подхода к оценке фактов меняется и интуиция. Основанная не на чувственном, а на научном знании, в частности, с использованием математических приемов, она становится средством движения вперед, к поиску новых знаний.
В чем же причина исключительной эффективности математики?
Почему возможно такое превосходное соответствие математики с реальными предметами и явлениями, если сама она является произведением человеческой мысли? Может ли человеческий разум без всякого опыта, путем только размышлений понимать свойства реальных вещей? Согласуется ли природа с человеческой логикой? Почему в тех случаях, когда явление понято нами и приняты соответствующие формулировки (аксиомы), сотни следствий оказываются столь же применимыми к реальному миру? Эти вопросы находятся в «списке» вечных вопросов философии науки. Всех, кто пытался разобраться с ними, а над этим задумывалось большое число мыслителей от древности до наших дней, по ответам можно условно разделить на 2 группы [1,2]. Первые считают, что математики подбирают аксиомы так, чтобы выводимые из них следствия согласовались с опытом, то есть - математика подстраивается под природу. Другими словами, всеобщие и необходимые законы опыта принадлежат не самой природе, а только разуму, который вкладывает их в природу, т.е. научную истину создают, а не находят. Вторые считают, что мир основан на математических принципах; в религиозном варианте – создатель построил мир на принципах математики. Среди и первых, и вторых много великих имен – этот вопрос нельзя обойти, если занимаешься исследованием природы. Естественна и незавершенность дискуссии – обсуждаемые вопросы не случайно в списке вечных проблем теории познания [3,4]. По Нильсу Бору, в похожих отношениях находятся точность модели и ее ясность. «…Наша способность анализировать гармонию окружающего мира и широта восприятия всегда будут находиться во взаимно исключающем, дополнительном соотношении» [5,6].
Литература
1. Соболев В.В. Валютный дилинг на финансовых рынках/ Юж.-Рос. гос. техн. ун-т (НПИ). – Новочеркасск, 2009. – 442 с.
2. Клайн М. Математика. Поиск истины. М.: Мир, 1988. 295 с.
3. Пуанкаре А. О науке. М.: Наука, 1983.
4. Малинецкий Г.Г. Хаос. Структуры. Вычислительный эксперимент (введение в нелинейную динамику). М.: Эдиторил УРСС, 2000. 256 с.
5. Бор Н. Избранные научные труды. Т. 2. М.: Наука, 1971.
6.Безручко Б.П., Смирнов Д.А. Математическое моделирование и хаотические временные ряды. Саратов: ГосУНЦ «Колледж», 2005. 320 с.






















