Стереотипность и адекватность математических моделей валютного курса

Неопределенность подстерегает трейдера на каждом торговом шаге, вынуждает принять ее как данность и попытаться снизить. В качестве количественной характеристики неопределенности в мире математических моделей выступает вероятность. Очевидно, что для ее получения необходимо заменить сложную проблему расчета вероятностей наступления того или иного события каким-нибудь простым и понятным правилом. Именно поэтому большинство людей в повседневной жизни полагается на стереотипы - эвристические подходы.

Эвристика — это совокупность исследовательских методов, способствующих обнаружению ранее неизвестного. В нашем случае эвристика — это подход к решению той или иной проблемы, основанный на интуиции и опыте человека.

Одним из наиболее распространенных отклонений связанных с вероятностным принятием решений, является репрезентативность —  суждение, основанное на стереотипах. Наиболее распространенными из них являются: FOREX  это легкий путь к обогащению и азартная игра, для людей из новичков, решивших "поиграть в FOREX".  Которые не имеют ни малейшего представления о том, каков механизм этой "игры", какими факторами вызваны изменения валютных курсов и т.п. Легких путей к обогащению не бывает и в конечном итоге, приходится трудиться в поте лица даже гениальным личностям в их стремлении "заработать" на трейдинге. Профессия трейдера может быть приравнена к творческим специальностям и научиться спекулировать быстро это из области фантастики.

Нет четких правил, по которым движутся цены. Конечно, существуют рынки, где вероятность правильного предсказания достаточно велика, например, на рынке золота, но и здесь случается непредсказуемое (рис. 1).

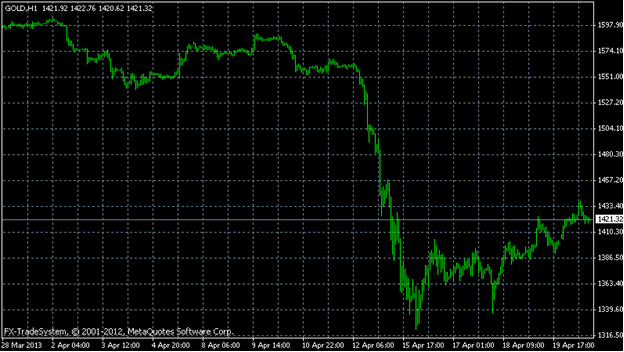
Рисунок.1  Часовой график золота

Математическое описание объекта может иметь различную степень соответствия - адекватности объекту-оригиналу. Как правило, при моделировании стремятся к более полному и точному отражению в модели свойств объекта. Это естественное стремление объясняется наличием неопределенности, которая неизбежно присутствует при построении моделей, так как  нельзя заранее точно знать, что именно используемые свойства объекта важны для решаемой задачи. Такая неопределенность тем больше, чем меньше опыт в решении подобных задач, да и валютный рынок невозможно описать адекватной физико-математической моделью. Потому что это “живое существо”, имеющее устойчивое, повторяющееся во времени слабо предсказуемое поведение. Но, если изучить повадки этого “существа”, то по некоторым признакам возможно предсказать будущее движение валютных курсов.

Валютный рынок это нелинейная динамическая система с очень большим количеством неизвестных характеристик, которые невозможно установить аналитическими методами. Это случайный процесс с неизвестными вероятностными (статистическими) параметрами, но со слабой детерминированной составляющей. Такое представление валютного рынка принято подавляющим большинством его участников.

Важнейшим требованием к математическому моделированию валютного курса является требование к ее адекватности – адекватному соответствию изучаемого реального объекта относительно выбранной системы его свойств. Под этим, прежде всего, понимается:

1) правильное качественное описание рассматриваемых свойств объекта. Например, возможность на основании исследования модели сделать правильный вывод о направлении изменения каких-либо количественных характеристик этих свойств, об их взаимосвязи, о характере колебаний объекта, об устойчивости его состояния или эволюции.

2) правильное количественное описание этих свойств с некоторой разумной точностью.

В зависимости от того, ставится ли второе условие или нет, говорят о количественных или качественных моделях. Вместо количественной адекватности говорят также о точности модели.

Подчеркнем, что адекватность следует рассматривать только по определенным признакам — свойствам. Если они явно не указаны, то должны подразумеваться, либо уточняться по ходу исследования. Поэтому термин «математическое моделирование» следует применять по отношению к области прикладной математики, включающей в себя как построение и исследование математических моделей, так и создание вычислительных алгоритмов и программ, реализующих эти алгоритмы. К примеру, математическое  моделирование системы трендовых индикаторов технического анализа и эвристические методы, основанные на использовании экспертных оценок; математическое моделирование валютного курса на базе аналитических зависимостей и факторов,  влияющих на валютный курс.

Можно сделать вывод: любая прогнозная модель движения валютных курсов должна включать огромное число переменных величин, и во всех случаях необходима надежная статистическая проверка, учитывающая перемещение факторов и случайность.

Академические институты осуществляли попытки построения адекватной математической модели прогнозирования валютных курсов, но всякий раз они не имели успеха. По мнению специалистов, в основе такой модели должна лежать теория паритета покупательной способности, но прогнозы валютных курсов, основанные на данных о денежной массе и доходах, дают значительные расхождения с реальностью. Однако возможно прогнозировать трендовую составляющую валютного курса и при создании системы поддержки принятия решений в задачах фундаментального анализа, и прогнозирования макроэкономической динамики и валютных курсов наряду с разработкой ее функциональной структуры, и информационным представлением процессов международного движения капитала, развития национальных экономик и финансовых рынков.

Таким образом, сложность развития макроэкономических процессов международного движения капитала, национальных экономик и финансовых рынков такова, что для решения задач идентификации и среднесрочного прогнозирования данных процессов и валютных курсов целесообразно применение адаптивных статистических моделей [1,3,4,5].

В.В.Соболев,

Институт финансового контроля и аудита

Литература

1. Соболев В. В. Валютный дилинг на финансовых рынках/ Юж.-Рос. гос. техн. ун-т (НПИ). – Новочеркасск, 2009. – 442 с.

2. Соболев В. В. Финансисты/ Юж.-Рос. гос. техн. ун-т (НПИ).–Новочеркасск, 2009.–315 с.

3. http://fortrader.ru/fortrader_archive/fortrader62/k-voprosu-adekvatnosti-matematicheskix-modelej-valyutnogo-kursa.html

4. Самарский А.А., Михайлов А.П. Математическое моделирование: Идеи. Методы. Примеры.- М.: Наука, 1997 – 320с.

5. Лукашин Ю. П. Адаптивные методы краткосрочного прогнозирования временных рядов: Учебное пособие. –  М.: Финансы и статистика, 2003. – 416 с.

6. Мишкин Ф. Экономическая теория денег, банковского дела и финансовых рынков: Учебное пособие для вузов/ Пер. с англ. Д.В. Виноградова под ред. М.Е. Дорошенко. – М.: Аспект Пресс, 1999. – 820 с.

7. Петерс Э. Фрактальный анализ финансовых рынков: Применение теории хаоса в инвестициях и экономике. – М.: Интернет-трейдинг, 2004. – 304 с.