Важным элементом системы поддержки принятия решений в задачах фундаментального анализа и прогнозирования макроэкономической динамики и валютных курсов является структуризация процессов международного движения капитала, развития национальных экономик и финансовых рынков. Также следует упомянуть и формирование схемы причинно-следственных связей их фундаментальных индикаторов, раскрывающей структурные особенности вышеуказанных процессов и возможные пути развития кризисных явлений. Стандартизированный перечень таких индикаторов, рекомендуемых информационными агентствами для оценки макроэкономической динамики и процессов экономического развития хорошо известен. Рассмотрим формализованные методы представления схемы их причинно-следственных связей.
В простейшем случае связи фундаментальных макроэкономических индикаторов формально могут быть описаны бинарными отношениями, или, что более наглядно, графами на заданном множестве фундаментальных индикаторов. Определяя фундаментальный индикатор как "объект", отметим, что бинарными отношениями (графами) охватывается лишь один достаточно специальный вид связей, а именно, связи типа "объект – объект". В действительности наряду с этим простейшим типом "парных" связей в исследуемой предметной области широко присутствуют "коллективные" или множественные связи, в которых участвуют более чем по два объекта. Это связи вида "группа объектов - группа объектов" или "объект - группа объектов". Пусть имеет место ситуация, когда некий объект "b" связан с объектом "a" определенным причинно-следственным отношением. Обозначим эту ситуацию как связь a → b ("a влияет на b"). Однако более значимым является выявление ситуаций, когда несколько объектов a1,…, an , взятые в совокупности, влияют на "b". Определим эту ситуацию как множественную связь типа "группа объектов - объект" и обозначим её как {a1,…, an } → b, или А → b, где А = {a1,…,an }. При этом в дальнейшем под причинно-следственной связью А → b будем понимать отношение следования ("b может быть проявлением влияния {a1,…,an }") или отношение совместимости ("изменение b сопровождается изменениями в {a1,…,an} в соответствии с некоторой функциональной зависимостью"). Структуру связей вида А → b будем называть частью ориентированного гиперграфа. Данный гиперграф – односторонний в том смысле, что его дуги всегда идут от множеств к одноэлементным вершинам. Определение необходимой совокупности и установление определённой упорядоченности таких гиперграфовых связей на всем множестве фундаментальных индикаторов анализируемой системы и составляет схему причинно-следственных связей фундаментальных индикаторов рассматриваемой предметной области.
Далее, опираясь на базовые положения теоретических разработок в области международной экономики, перейдём к определению основных гиперграфовых связей на множестве фундаментальных индикаторов, характеризующих взаимосвязанные процессы международного движения капитала, развития экономик и финансовых рынков, применительно к анализу динамики такого значимого для международной экономики показателя как валютный курс EUR/USD (рис. 1).
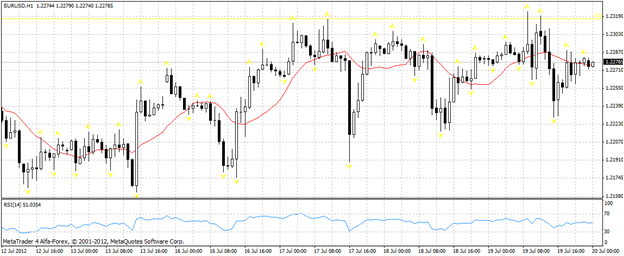
Рисунок 1. Динамика валютного курса EUR/USD
Текущий обменный курс той или иной валюты определяется соотношением её спроса и предложения на международном валютном рынке. При этом множество факторов, определяющих спрос и предложение, можно разделить на три группы: торговые операции, связанные с экспортом и импортом товаров и услуг; спекулятивные операции с капиталом; неспекулятивные операции с капиталом, что дает возможность построить простую концептуальную модель системы свободно плавающих обменных курсов вида
( ↓ТВ, ↑S, ↑N ) → ↓ E, ( 1)
где: ТВ – торговый баланс ( ↑ = профицит, ↓ = дефицит), S – спекулятивное движение капитала; N – неспекулятивное движение капитала ( ↑ = рост вывоза капитала, ↓ = рост ввоза капитала); Е – номинальный обменный курс ( ↓ E – ослабление курса национальной валюты). Причины движения капитала, отражаемого в приведенной модели, могут быть разнообразными. Однако главной из них является поиск более высокого общего уровня дохода на вложенный капитал, а именно: получение дохода от экспортных операций, получение дохода на разнице в процентных ставках по депозитам и кредитам, разнице в текущей доходности таких значимых финансовых активов как государственные облигации, корпоративные ценные бумаги и др. Что позволяет построить более расширенную концептуальную схему влияния вышеуказанных фундаментальных индикаторов на соотношение спроса и предложения на валютные активы, а соответственно и на обменный курс.
Из сказанного следует вывод, что наличие механизмов усиления/ослабления динамики индикаторов в контурах с обратной связью, присутствующих в схемах и модели (1), может с учетом сложности их взаимодействия и меняющихся по силе влияний индикаторов в этих контурах приводить к возникновению неустойчивости исследуемой системы. Очевидно, что учет данных особенностей позволяет осуществлять анализ и прогнозирование развития процессов в системах рассматриваемого типа более качественно по сравнению с существующими подходами, связанными с локальным анализом того или иного фрагмента системы.
В.В.Соболев
Южно-Российский государственный технический университет
Литература
1. Соболев В.В. Валютный дилинг на финансовых рынках/ Юж.-Рос. гос. техн. ун-т (НПИ). – Новочеркасск, 2009. – 442 с.
2. Мишкин Ф. Экономическая теория денег, банковского дела и финансовых рынков: Учебное пособие для вузов/ Пер. с англ. Д.В. Виноградова под ред. М.Е. Дорошенко. – М.: Аспект Пресс, 1999. – 820 с.
3. http://uk.fortrader.ru/fortrader_archive/61-nomer-zhurnala/analiticheskie-metody-matematicheskogo-modelirovaniya-valyutnogo-kursa.html
4. http://dissers.ru/avtoreferati-dissertatsii-ekonomika/a489.php






















