Когда речь идет о состоятельности торговых результатов того или иного трейдера или результатов тестирования на истории определенной торговой стратегии, зачастую принимают во внимание результаты с учетом волатильности или просадки. Тем не менее, данный подход не может в полной мере определить состоятельность и значимость результатов торговли.
Длинные периоды пониженной волатильности, флетообразные (горизонтальные) движения в диапазоне, естественно, нежелательны, но имеют место быть и не отображены в коэффициентах Sharpe и MAR .
Вместо этого нам стоит обратить внимание на более специализированный “прямолинейный” подход к определению состоятельности торговых результатов.
Конечно же, есть и стандартные подходы. Самый популярный из них - R-squared (показатель R, возведенный в квадрат). И, нужно отметить, он работает достаточно хорошо. Хотя предпочтительней использовать возведение в четвертую степень вместо квадрата, чтобы увеличить контраст даже в пределах незначительных изменений и сделать результаты более удобочитаемыми.
Еще одним популярным способом измерения является K-Ratio (коэффициент К). В сети можно найти 3 версии. K-Ratio не является 100% прямолинейным подходом, так как учитывает и возврат от инвестиций, лучше использовать Зефир-версию (Zephyr version).
Теперь давайте попробуем создать некоторую альтернативу имеющимся подходам.
Чтобы начать, нам нужна своеобразная база или отправная точка, относительно которой будет происходить измерение. Будем называть ее ИДЕАЛЬНАЯ ЛИНИЯ (ИЛ). Это прямая линия, соединяющая начало и конец кривой (рис. 1) . Чем сильнее кривая отклоняется от этой прямой, тем это менее желательно.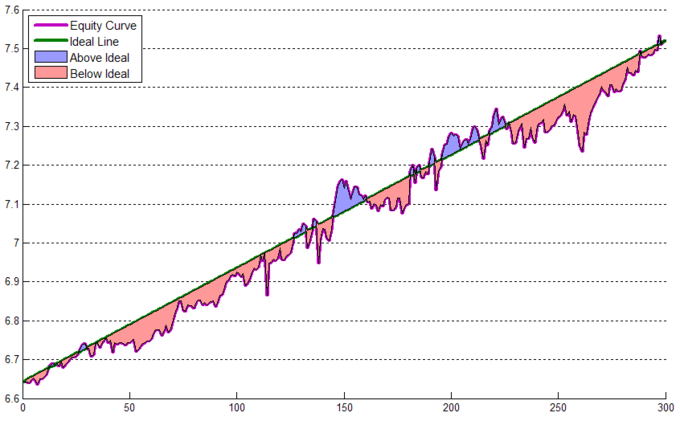
Рисунок 1. Идеальная линия
Теперь поговорим о кривой, а также идеальной линии и различиями между ними.
Из этого простого типа анализа можно вывести несколько очевидных принципов:
-
Мы стремимся к тому, чтобы минимизировать область отклонения от ИЛ
-
Чем дальше наши показатели находятся от ИЛ, тем хуже
-
Лучше быть над ИЛ, чем под ней
-
Нежелательно находиться под ИЛ долгое время
Мы запросто можем перевести эти принципы в количественные показатели, включая общую площадь отклонения от ИЛ, волатильность этого отклонения, продолжительность пребывания под ИЛ и т.д. Также следует обратить внимание на количество пересечений кривой и ИЛ.
Аналогично, мы можем измерять среднюю продолжительность просадки. Возможно, этот показатель даже более важен, потому что продолжительные отклонения от ИЛ вниз более важны, чем отклонения от ИЛ вверх, а показатель количества пересечений кривой и ИЛ не разделяет их на бычьи и медвежьи.
Также стоит обратить внимание на соотношение между площадями отклонений вверх и вниз от ИЛ, волатильность этой разницы и волатильность отклонения вниз, а также абсолютное среднестатистическое отклонение и абсолютное среднестатистическое отклонение вниз от ИЛ
Измерительный принцип, объединяющих некоторые из вышеупомянутых концепций следующий: QUSMA Equity Curve Straightness, Downward Deviation, and Stability Measure (QECSDDSM)
Вот его формула: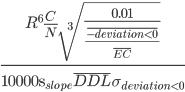
Теперь несколько примеров (рис. 2 и 3):
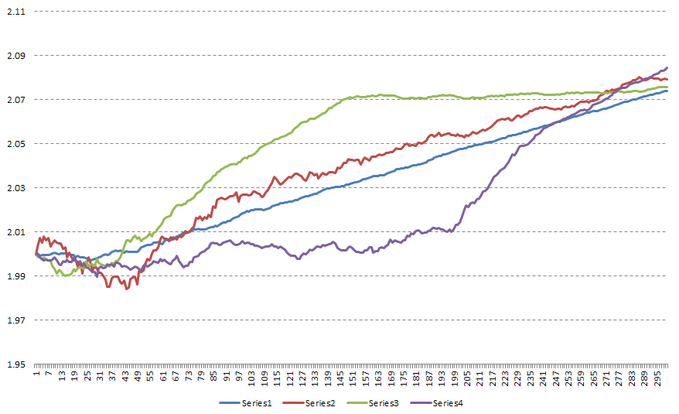
Рисунок 2. Идеальная линия: пример 1
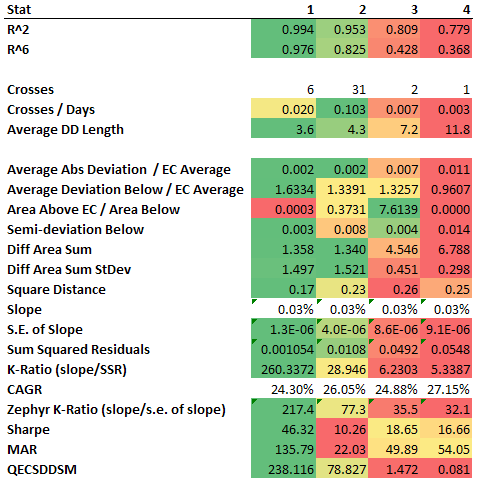
Рисунок 3. Расчет коэффициентов для измерительного принципа: пример 1
Во-первых, обратите внимание, что оба коэффициента (Sharpe и MAR) выбирают неправильную стратегию при использовании со стандартными настройками (оба предпочитают серию 3 & 4 вместо серии 2).
Как коэф K-Ratio так и QECSDDSM предпочитают первые два. Обратите внимание что количество пересечений не имеет значения в этом случае, так как оптимальная линия содержит минимальное количество таких пересечений. Соотношение площадей отклонений вниз и вверх от ИЛ также имеет в данном случае маленькую ценность из-за экстремальных значений.
В общем, большая часть данных приблизительно согласуется друг с другом в плане расположения кривых от лучшего к худшему. Поэтому фактическая формулировка QECSDDSM на самом деле не имеет значения. Теперь посмотрим на немного более реалистичную выборку кривых (рис. 4 и 5):
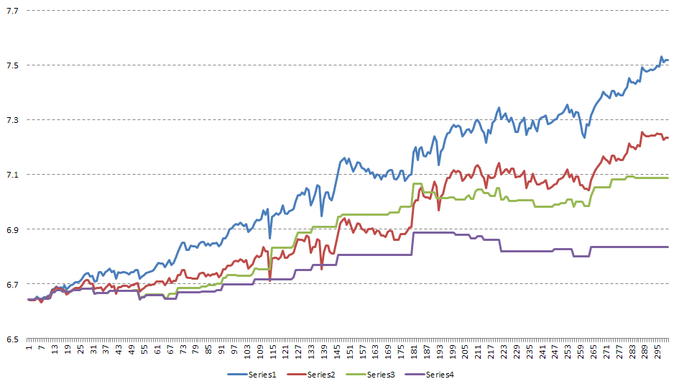
Рисунок 4. Идеальная линия: пример 2
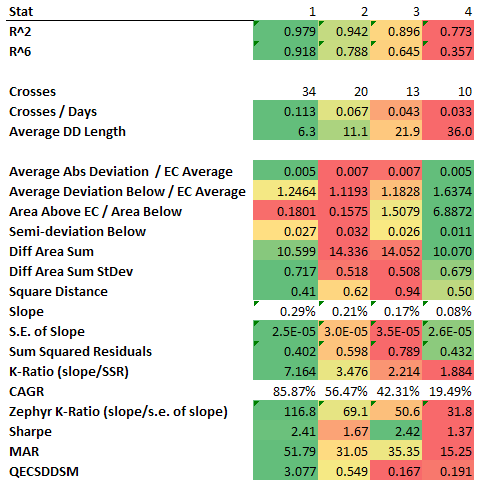
Рисунок 5. Расчет коэффициентов для измерительного принципа: пример 2
В этом случае логика, стоящая за данными числами, выглядит вполне очевидной. Интересен тот факт, что QECSDDSM является единственным показателем, предпочитающим серию 4 серии 3, что, как нам кажется, нежелательно.
Серия 4 подчеркивает проблему с измерением волатильности или вниманием на отклонениях вниз от ИЛ. Даже небольшое количество торговых позиций генерирует слишком высокие значения.
Коэффициенты Sharpe и MAR опять генерируют неверные данные, так как предпочитают серию 3 серии 2.
Разница в основном происходит от того, что кривая не слишком волатильна и не проводит слишком много времени под ИЛ. Если поиграть с настройками немного, можно сгладить данные.