Андрес Навас, математик из Университет де Сантьяго де Чили, продемонстрировал очередное наглядное и простое доказательство теоремы Пифагора. Препринт, посвященный исследованию, автор обнародовал на странице arXiv.org.
Теорема Пифагора говорит, что в прямоугольном треугольнике (точнее, треугольнике, который имеет прямой угол) квадрат гипотенузы (большей стороны, что находится напротив угла в 90 градусов) равен сумме квадратов катетов (двух других от гипотенузы меньших сторон). На сегодняшний момент предоставлено свыше 350 разных доказательств данного утверждения.
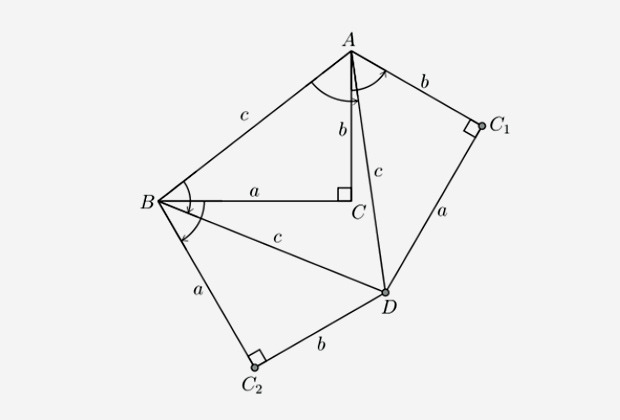
Навас применил теорему Бойяи — Гервина, что утверждает равносоставленность двух любых равновеликих многоугольников. Специалист производит два разворота треугольника АВС: первый — в отношении точки А на угол в 60 градусов против стрелки часов, другой — вокруг точки В, на угол в 60 градусов по стрелке часов. После этого Навас проводит расчет площади получившегося многоугольника, что состоит их двух многоугольников, которых площади равняются площади треугольника АВС, и равностороннего треугольника со стороной С, откуда и приводит необходимое утверждение.
Теорема Пифагора, как уверяет в книге «Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции» математик и историк науки Голландии Бартель ван дер Варден, известна была еще в восемнадцатом веке до нашей эры населению Вавилона, также как и индийцам, и египтянам. Обширную популярность она получила после написания 13 книг «Начал» Евклида, где в завершении первой книги описывается и доказывается теорема Пифагора.
Как домохозяйка сделала научное открытие.
Математика современности все менее доступна для известного изложения. Это имеет связь с тенденцией, что восходит еще к программе Николя Бурбаки, которая предполагает аксиоматическое изложение, основываясь на теории множества самой точной из науки и отказ от геометрического описания в сторону алгебраического.
Невзирая на экстремальное увеличение степени абстракции математики нынешнего дня, в данной древней науке по сей день отмечаются открытия, смысл которых понять можно сразу.
Последнее из подобного — новый вид пятиугольного паркета: выпуклые пятиугольники, которыми предоставляется возможность замостить плоскость без наложений и пробелов. Эта статья была включена в перечень лучших публикаций прошлого года.
Поиск и классификация многоугольных паркетов считаются наглядным и интересным заданием теории замощений нынешней комбинаторной геометрии. К текущему времени математики знают, что любым треугольником и четырехугольником можно замостить плоскость, а вместе с этим, что присутствуют только три варианта выпуклых шестиугольников, имеющих возможность это сделать (многоугольник выпуклый, если он находится по одну сторону от прямой, что содержит любую его сторону).
